(Or, “regularized greedy algorithms and their applications.”)

James Gilles

“Algorithm” is one of those words that sounds fancier than it really deserves. We hear all the time about the “facebook algorithm”, the “youtube algorithm”, “high frequency trading algorithms”, “artificial intelligence algorithms”, and so on. What are these, really?

The “facebook algorithm” is a large blob of software that Facebook uses to try to get people to stay on their website longer. It’s a complicated and expensive machine designed to extract user data and sell ads. All the social media “algorithms” boil down to that. Money making machines, based on a lot of loose guesses and elbow grease.

A broader meaning of “algorithm” is “detailed strategy to accomplish something.” There’s a whole field of study dedicated to analyzing such things mathematically (computer science), but you don’t have to learn math to study them. In fact, they abound in everyday life. Everybody’s got their own collection of algorithms. How do you crack your eggs, sort your books, tie your shoelaces?

I recently came across a particularly lovely everyday algorithm. This youtube video gives the following strategy for untangling headphone wires:

You might not believe that this works, so here’s a video of me trying it:

Like magic, they unfurl. There is some care involved, though. If you pull too hard, you can knot them up worse:

And if you shake without pulling, you won’t accomplish much:

But when you do both at the same time, in the right ratio, it works surprisingly well. What’s going on here? How can such a simple approach yield such good results?

Let’s study the ingredients. What does the pulling do? I would say that the pulling encourages the system to stretch out. (By “system” I just mean “headphones”.)

What does this have to do with untangling? Well, tangles keep the system from stretching out fully. For the system to be as stretched out as you can get, you need to get rid of the tangles. But we can’t be too direct about it. Simply pulling on the wires knots them into a tight ball, and we get stuck.

How do we avoid getting knotted up? Shaking as we pull does something interesting. It encourages the system to explore more possibilities, by giving the wires motion and energy – lives of their own. Lively wires are less inclined to get knotted up. I think of them as being slipperier or blurrier. In a thermodynamic sense, you could say that they’re hotter – that is, they have a lot of diffuse kinetic energy – that is, they’re wiggling around.

Each second, each wiggling wire explores many different configurations. Where two motionless wires tend to get knotted up, two moving wires are more likely to find a configuration that allows them to slip past each other. This added flexibility allows the system to slip past sticking points, on its way to being fully stretched out.

Interesting enough. So what?

This idea – gently pulling a system in some direction, while adding in random shaking or smoothing – actually underlies many computer algorithms as well. That video I linked earlier does a great job of explaining this metaphor for one particular problem. But it’s actually really broadly applicable, and I wanted to riff on it a while.

In particular, it’s broadly applicable to algorithms that solve “hard” problems. What does “hard” mean? Computer science has many different mathematical models for studying and comparing computations – asking questions like, “if you increase the amount of input data, how much more time do you need to solve it?” For easy problems, you don’t need much extra time; for hard problems, you need lots of extra time.

Some examples of easy problems are:

• Sorting lists of numbers
• Searching through sorted tables of data
• Finding paths through road maps

Some examples of hard problems are:

• Laying out circuits to minimize production costs
• Training neural networks (“AIs”) to recognize images
• Solving logic puzzles with thousands of variables

Ignoring the mathematical models, my rough rule of thumb is that “easy” problems generally take a fraction of a second on a modern computer, where “hard” problems take hours or days. But there are more differences than mere time and space.

See, you start your computer science degree with an Algorithms 101 class, which is about techniques for solving easy problems. These techniques have a generally reductionist flavor. Given a problem, you break the problem into parts, solve each part separately, and then combine the solutions.

(Merge sort comes to mind:

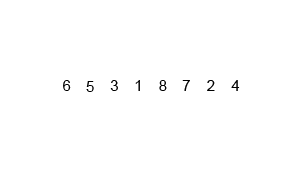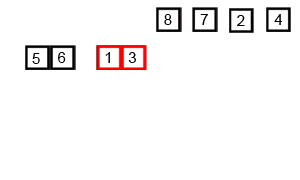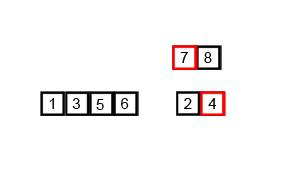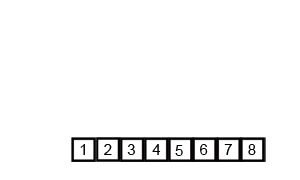
The basic idea is that you can combine two sorted lists of numbers by comparing the elements at the front and pulling off the smaller one. This gives you a sorted list of all the elements in both lists. This algorithm is called “merge”.

But if we start with an entirely unsorted list, how can we find sorted lists? Simple, break it into single elements, which are “sorted”, and then repeatedly apply “merge” to build up bigger and bigger runs of sorted numbers.)

I find understanding this sort of algorithm very satisfying. It gives me a feeling of power, like I’m designing a factory production line, and know precisely what each machine involved has to do.

But when you get out of algorithms 101, you quickly run into problems where this sort of approach isn’t possible. These problems are more than the sums of their parts – different parts of the system interact with each other, and you can’t study them in isolation anymore.

For example, laying out circuits. For very complicated circuits like CPUs, engineers don’t typically start by designing a physical layout of the circuit. Instead, they just specify components and their connections by name; component A links to component B which links to component D, there is a batch of component E’s connected to each other in a daisy chain, etc. (This is usually done in a hardware description language.)

The problem is to pick locations for components, and then connect them with wiring, while minimizing how much space the wiring takes up (since circuit space is expensive.) This is called Place and Route.

But this sort of problem isn’t amenable to reductionist solutions. You can’t divide the circuit into chunks, lay them out in efficient ways indidually, and then link them together – because the cross links take up space too, but you might not have left room for them! Maybe you bump some of your old links out of the way – but oops, now they’re intruding on space that was used for something else! And so on.

You can’t solve the problem in parts; you have to solve it all at once, because its parts are all tangled up. But how can we possibly do such a thing?

The answer, of course, is “shake and pull gently”. You start by making a very bad layout that takes up way, way more space than it needs; this is relatively easy to do. Then, you randomly wiggle the wires of your design, while pulling them tight to take up less space. You do this for a while, slowly decreasing your wiggling and increasing your pulling, and you stop when the circuit is small enough to satisfy you.

This algorithm is called simulated annealing. Here’s a graphic of it; in this case it’s trying to find the shortest path through all the dots that goes through each dot exactly once:'

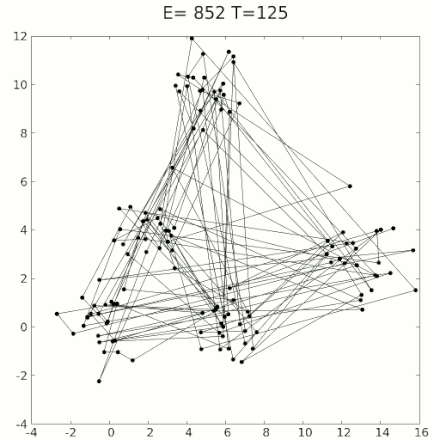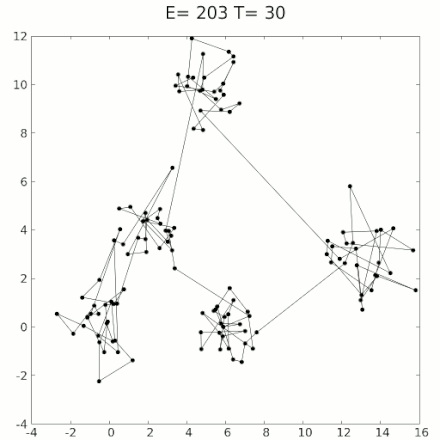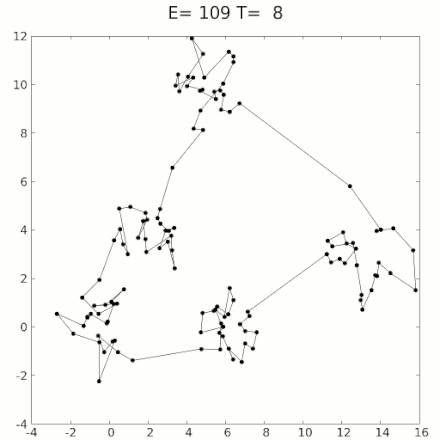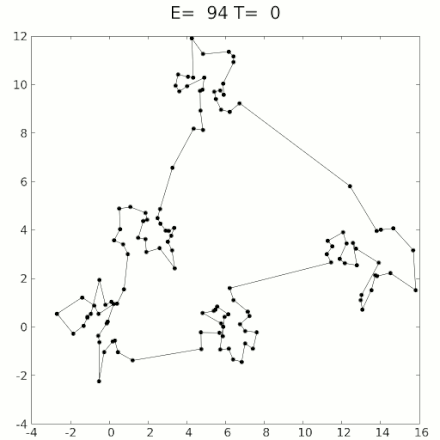
You may notice that this example is not moving smoothly, like headphone wires, but instead is proceeding in discrete jumps. Simulated annealing for circuits is similar: Circuit wires are often constrained to be laid out on a grid, and can’t move smoothly. So instead, you apply small random jumps, moving bits of wire from one grid corner to another. This acts as “shaking”.

Also, before you do any jump, you ask: will this improve or worsen the cost of the the chip? If the answer is “improve”, you do the jump; but if the answer is “worsen”, you don’t always reject it. Instead, you flip a coin. On heads, you do the jump anyway. That is, you sometimes accept “bad” random jumps, which make the chip more expensive.

This might seem counter-productive, but it’s how we implement “shake and pull gently” in a non-bendy setting. If you never accepted bad jumps, it would be like pulling your headphone without shaking: all the “good” jumps would quickly get applied. But then there might be many more improvements available, just not immediately.

Accepting bad random jumps encourages the system to explore many more possibilities. But we’re still weighting the dice, so to speak; good jumps are more likely to be applied than bad. So the system tends to drift in a good – less expensive – direction.

The algorithm is called “simulated annealing” because you typically start with a high bad-accept chance and then lower it over time. “Annealing” is a process where you heat slowly and cool metal to harden it. A high bad-accept chance is like a high temperature, because it induces more random motion; a low bad-accept chance is like a low temperature, because it doesn’t. By heating the system hot and slowly cooling it, you encourage it to loosen up and then slowly converge to a good solution.

You might notice that this is by no means guaranteed to actually work – that is, find a solution you like. It could just get stuck, spit out something worse than you put into it. This is something I was very uncomfortable with when I started studying hard problems: if there’s no guarantee it’ll work, how can you trust your algorithm?

This is a general theme in hard problems. Solving them is less like designing a factory and more like baking: you have to know your ingredients well, and combine them correctly; but after a certain point, all you can do is wait and pray.

Broadly speaking, there are far too many possible solutions to check if any given answer is the absolute best answer. You can only compare your solution with other, “nearby” solutions (e.g. solutions a single jump away). So instead of asking, “is this the best possible answer?”, you simply ask, “is this answer good enough?”

And in fact, in practice, the answer often is good enough. This approach is used to lay out many of the hyper-complex computer chips we use every day. And, if you squint, you can see the bones of this algorithm in many other hard problems. I’ll run through a quick battery of examples. (I’m going to skimp on intuitive explanation here, because when I tried to explain each of these in detail it added a few thousand words to the article, and nobody has time for that… I’ll probably come back and talk about deep neural networks more in a later post. They’re near and dear to my heart, like a clogged artery.)

• Deep neural networks, trained to imitate a dataset with stochastic gradient descent: “gradient descent” involves “pulling” on the tuning parameters of a statistical model to make them approximate some dataset. “Stochastic” gradient descent involves randomly sampling sub-chunks of the dataset to approximate at a time. This random sampling acts like “shaking”, and the gradient descent part acts like “pulling”.
• Genetic algorithms: often used to explain deep neural networks, although they aren’t actually used much anymore. But the analogy is close enough: genetic algorithms are like a slightly more complex version of simulated annealing, with a population of candidate solutions being randomly mutated instead of just a single one. (You could argue that biological evolution is a “shake and pull gently” algorithm, but I’m not sure I’d agree; biological evolution doesn’t actually have a goal, it’s just that whatever reproduces, reproduces, and whatever doesn’t, doesn’t…)
• SAT / SMT solvers: Maybe calling backtracking search “shake and pull gently” is pushing it, since there isn’t any explicit randomness involved, but I think the analogy still works; you just have to view exhaustive search as a generalized form of random sampling.

(Actually you can do without random sampling in neural networks as well, but you have to add in other ingredients that approximate its smoothing effects. So what matters more than the random shaking itself is how the random shaking smooths and simplifies the problem. You could call it a “good rule of thumb for making the problem more regular”; machine learning experts call such things “regularization heuristics”, because if you don’t use long words you can’t get research funding.)

By the way, a “greedy algorithm” is just an algorithm that blindly makes small improvements to a solution without thinking very hard about them. The byline of this post was “regularized greedy algorithms and their applications”; now we can say what a “regularized greedy algorithm” actually is. It’s an “algorithm that blindly moves in a direction while trying not to get stuck.” Or, more simply, “pull and shake gently”.

Stated so bluntly, maybe it’s obvious why such things have broad applications. Did this really deserve a whole 2000-word post? Well, here we are.

I hope this helps demystify “algorithms”; whenever you see a headline about “algorithms”, there’s a good chance it boils down to “shake and pull gently”. It may be worth questioning whether we should trust “shake and pull gently” to select what news stories we read, whether we receive home loans, or whether we are drone striked as a terrorists. Especially when the “pull gently” part of the algorithm is attempting to optimize the profits of Facebook, Wells Fargo, or Raytheon, respectively.

Postscript:

It occurs to me that there’s something I oughtta admit. It actually took me a bunch of tries to get that shot of the headphones coming untied. Most of the times I tried it didn’t work, or only worked partially, leaving me with some knots to undo by hand. Even if I can describe the technique in a simple way, actually applying it takes practice and skill.

That applies to all the algorithms I’ve talked about here. Neural networks, SMT solvers, Place & Route engines; none of these things are straightforward. The devil is in the details, and getting to know such details can be a life’s work. I don’t want to denigrate that work; just point out some shared themes.